Lagrange Multiplier

Lagrange Undetermined Multipliers

If the constraints contain the velocity terms $$f_\alpha(q_1,...,q_n;\dot{q}_1,...,\dot{q}_n)=0,\tag{1}$$ the constaints are called semi-holonomic. The index \(\alpha = 1,2,...,m\) indicates the number of constraint equations.

To eliminate the extra virtual displacements, a method called Lagrange undetermined multipliers was introduced. If condition of semi-holonomic hold, then $$\sum^m_{\alpha=1}\lambda_{\alpha}f_{\alpha}=0,$$ where \(\lambda_{\alpha}\) are undetermined quantities for each contraint equations. Hamilton's principle is assumed to hold in semiholonomic system as well such that $$\int^{t_2}_{t_1} dt\sum_k\left(\frac{\partial L}{\partial q_k}-\frac{d}{dt}\frac{\partial L}{\partial \dot{q}_k}\right)\delta q_k=0.$$ But the \(q_k\) terms are not all independent so it cannot be taken out as individual equations before. However, since Hamilton's principle is assumed to hold, we have $$\delta\int^{t_2}_{t_1}L dt = 0.$$ So, $$\delta\int^{t_2}_{t_1}\left(L + \sum^m_{\alpha=1}\lambda_{\alpha}f_{\alpha}\right)dt = 0.$$ The resulting equations from \(\delta q_i\) become $$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}_k}\right)-\frac{\partial L}{\partial q_k}=Q_k,$$ where $$Q_k=\sum^m_{\alpha=1}\left[\lambda_{\alpha}\left(\frac{\partial f_{\alpha}}{\partial q_k}-\frac{d}{dt}\frac{\partial f_\alpha}{\partial \dot{q}_k}\right)-\frac{d\lambda_{\alpha}}{dt}\frac{\partial f_{\alpha}}{\partial \dot{q}_k}\right].$$ The Lagrange multiplier method can used be when

• non-holonomic constraints in the form of (1)
• holonomic contraints with independent coordinates
• it is wished to obtain the constraint forces

Example (Goldstein p.49-50)

A hoop rolling without slipping down an inclined plane. Find the friction force of constraint.

Solution: The constraint is $$rd\theta = dx.$$ The kinetic energy is $$T=\frac{1}{2}M\dot{x}^2 + \frac{1}{2}Mr^2\dot{\theta}^2,$$ and the potential energy is $$V=Mg(l-x)\sin\phi.$$ So, the Lagrangian is $$L = T-V=\frac{M\dot{x}^2}{2}+\frac{Mr^2\dot{\theta}^2}{2}-Mg(l-x)\sin\phi.$$ Note that the friction of constraint is not included in the Lagrangian. Since there is only one constraint, there will be only one Lagrange multiplier \(\lambda\). \begin{align} Q_{\theta} &= r\\ Q_x &= -1. \end{align} The Lagrange equations are \begin{align} M\ddot{x} - Mg\sin\phi + \lambda &= 0\\ Mr^2\ddot{\theta} - \lambda r &= 0. \end{align} Taking time derivative on the constraint equation, we have $$r\ddot{\theta}=\ddot{x}.$$ So, $$M\ddot{x}=\lambda.$$ The friction force of constraint is $$\lambda = \frac{1}{2} Mg \sin\phi$$

Checkpoint

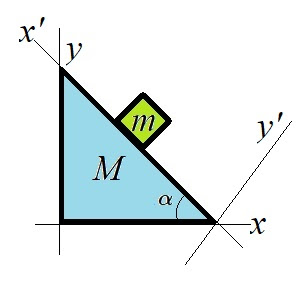
A block of mass m is placed on a frictionless incline of mass M, which is placed on a frictionless horizontal surface. Both the block and the incline are at rest. At time t=0, they are released to move freely. Using the method of Lagrange multiplier, find the equations of motion of the block and the incline.

The coordinates of the block are given by \begin{align} x &= x' \cos \alpha + x_M \\ y &= x'\sin\alpha . \end{align} So, the constraint is $$\frac{y}{x-x_M}=\tan \alpha.$$ Then we have \begin{align} Q_y &= \frac{\lambda}{x-x_M}\\ Q_x &= -\frac{\lambda_y}{(x-x_M)^2}\\ Q_{x_M} &= \frac{\lambda_y}{(x-x_M)^2}. \end{align} Substitute these into the Lagrange's equations, we have \begin{align} m\ddot{x} &= -\frac{\lambda}{(x-x_M)^2}=-\frac{\lambda\tan\alpha}{x-x_M}\\ m\dot{y}-mg&=\frac{\lambda}{x-x_M}\\ M\ddot{x}_M &= \frac{\lambda y}{(x-x_M)^2}=\frac{\lambda\tan\alpha}{x-x_M}. \end{align} From these equations, we have the relation $$\ddot{x}_M=-\frac{m}{M}\ddot{x}.$$ From the constraint, we have $$\ddot{y} = \tan\alpha(\ddot{x}-\ddot{x}_M).$$ Substitute this back, $$\tan\alpha(\ddot{x}-\ddot{x}_M)-g=\frac{\lambda}{m(x-x_M)}$$ we obtain $$\lambda = m(x-x_M)[\tan\alpha(\ddot{x}-\ddot{x}_M)-g].$$ Substitute \(\lambda\) and the relation \(\ddot{x}_M=-m\ddot{x}/M\) back into the equations of motion, we have \begin{align} m\ddot{x} &=-m\tan\alpha\left[\tan\alpha\left(\ddot{x}-\left(-\frac{m}{M}\ddot{x}\right)\right)-g\right]\\ \ddot{x} &= \frac{Mg\sin\alpha\cos\alpha}{M+m\sin\alpha}\\ \ddot{x}_M &= -\frac{m}{M}\ddot{x} = -\frac{mg\sin\alpha\cos\alpha}{M+m\sin\alpha} \end{align}