Quantum Harmonic Oscillator
Adjoint Operator
Let \(\hat{\theta}\) and \(\hat{\theta^{+}}\) be two operators. If $$\int f^*\hat{\theta^{+}}g dx = \int \left(\hat{\theta}f \right)^* g dx$$ then \(\hat{\theta^{+}}\) is the adjoint operator of \(\hat{\theta}\).If $$\hat{\theta^{+}} = \hat{\theta}$$ then the operator is an Hermitian operator.
Ladder Operators
$$\hat{H} = \left(\frac{\hat{p}^2}{2m} + \frac{1}{2}m\omega \hat{x}^2\right)$$ Define $$x_0 = \sqrt{\frac{2\hbar}{m\omega}}$$ and $$p_0 = \sqrt{2\hbar\omega m}$$ So, the energy operator can be expressed as $$\hat{E} = \left[\left(\frac{\hat{x}}{x_0} \right)^2 + \left(\frac{\hat{p}}{p_0}\right)^2 \right]\hbar\omega$$ Factorize \begin{align} \left(\frac{\hat{x}}{x_0} \right)^2 + \left(\frac{\hat{p}}{p_0}\right)^2 &= \left(\frac{\hat{x}}{x_0} - i\frac{\hat{p}}{p_0} \right) \left(\frac{\hat{x}}{x_0} + i\frac{\hat{p}}{p_0} \right) - \frac{i}{x_0p_0}[x,p] \\ &= \left(\frac{\hat{x}}{x_0} - i\frac{\hat{p}}{p_0} \right) \left(\frac{\hat{x}}{x_0} + i\frac{\hat{p}}{p_0} \right) - \frac{i}{2\hbar}(i\hbar) \\ &= \left(\frac{\hat{x}}{x_0} - i\frac{\hat{p}}{p_0} \right) \left(\frac{\hat{x}}{x_0} + i\frac{\hat{p}}{p_0} \right) + \frac{1}{2} \\ \end{align} Define $$\hat{a} = \frac{\hat{x}}{x_0} + i\frac{\hat{p}}{p_0}$$ Its adjoint operator is $$\hat{a^{+}} = \frac{\hat{x}}{x_0} - i\frac{\hat{p}}{p_0}$$ The energy operator can be written as $$ \bbox[5px,border:2px solid #666]{ \hat{E} = \hbar \omega(\hat{a^{+}}\hat{a} + \frac{1}{2}) }$$Commutator of Ladder Operators
The commutator of adjoint ladder operator and the ladder operator is \begin{align} [\hat{a},\hat{a^{+}}] &= \hat{a}\hat{a^{+}} - \hat{a^{+}}\hat{a} \\ &= \left(\frac{\hat{x}}{x_0} + i\frac{\hat{p}}{p_0}\right) \left(\frac{\hat{x}}{x_0} - i\frac{\hat{p}}{p_0}\right) - \left(\frac{\hat{x}}{x_0} - i\frac{\hat{p}}{p_0}\right) \left(\frac{\hat{x}}{x_0} + i\frac{\hat{p}}{p_0}\right) \\ &= \frac{1}{2} - \left(-\frac{1}{2}\right) \\ &= 1 \end{align} The commutator of the energy operator and the ladder operator is \begin{align} [\hat{E},\hat{a}] &= \hat{E}\hat{a} - \hat{a}\hat{E} \\ &= \hbar \omega\left[(\hat{a^{+}}\hat{a} + \frac{1}{2})\hat{a} - \hat{a}(\hat{a^{+}}\hat{a} + \frac{1}{2})\right] \\ &= \hbar \omega \left(\hat{a^{+}}\hat{a} - \hat{a}\hat{a^{+}} \right)\hat{a} \\ &= \hbar \omega (-1) \hat{a} \\ &= -\hbar \omega \hat{a} \end{align} The commutator of the energy operator and the adjoint ladder operator is \begin{align} [\hat{E},\hat{a^{+}}] &= \hat{E}\hat{a^{+}} - \hat{a^{+}}\hat{E} \\ &= \hbar \omega\left[(\hat{a^{+}}\hat{a} + \frac{1}{2})\hat{a^{+}} - \hat{a}(\hat{a^{+}}\hat{a^{+}} + \frac{1}{2})\right] \\ &= \hbar \omega \left(\hat{a^{+}}\hat{a} - \hat{a}\hat{a^{+}} \right)\hat{a^{+}} \\ &= \hbar \omega \hat{a^{+}} \end{align}Eigenvalues of Energy Operators
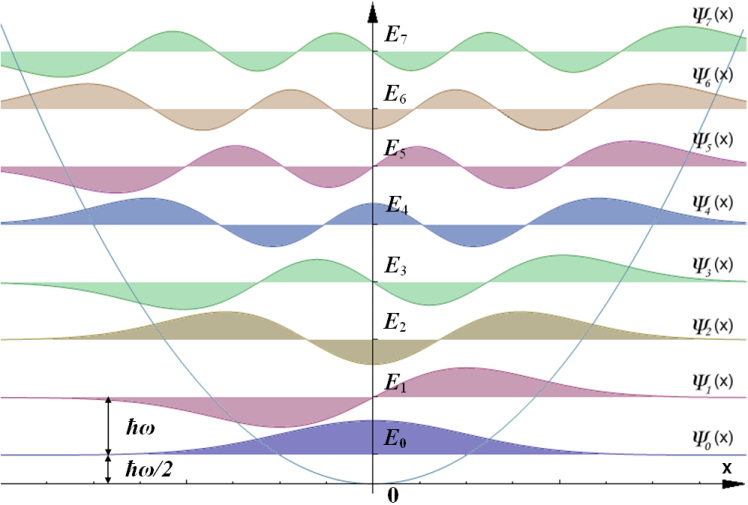
Let \(\phi_n\) be the eigenstate of the energy operator of the harmonic oscillator, and \(E_n\) be the corresponding eigenvalue $$\hat{E}\phi_n = E_n \phi_n.$$ We know that \(a\phi_n\) is also an eigenstate of this energy operator, $$\hat{E}a\phi_n = (E_n - \hbar\omega) a\phi_n,$$ with an eigenvalue \(E_n - \hbar\omega\). We denote the eigenstate with an eigenvalue \(E_n - \hbar\omega\) by \(\phi_{n-1}\), such that the equation is rewritten as, $$\hat{E}\phi_{n-1} = (E_n - \hbar\omega)\phi_{n-1}.$$ We repeat this operation until the lowest state (ground state) is reached \begin{align} \hat{E}\phi_n &= E_n \phi_n \\ \hat{E}\phi_{n-1} &= (E_n - \hbar\omega)\phi_{n-1} \\ .\\ .\\ .\\ \hat{E}\phi_0 &= (E_n - n\hbar\omega)\phi_0. \end{align} Now, we express the energy operator in terms of the ladder operators $$\hbar\omega(\hat{a}^\dagger a+\frac{1}{2})\phi_0 = (E_n - n\hbar\omega)\phi_0.$$ Since we know \(a\phi_0 = 0\), we have $$(E_n - n\hbar\omega - \frac{1}{2}\hbar\omega)\phi_0 = 0.$$ If we have a non null solution \(\phi_0\), we infer that $$\bbox[5px,border:2px solid #666] { E_n = \left(n + \frac{1}{2}\right)\hbar\omega }$$Finding Solutions
Let \(\phi_E\) be an eigenstate of the energy operator. $$\hat{E} \phi_E = E\phi_E$$ Let \(\psi\) be the resulting function after applying ladder operator on \(\phi_E\) $$\hat{a}\phi_E = \psi$$ Apply the energy operator on \(\psi\) \begin{align} \hat{E}\psi &= \hat{E}\hat{a}\phi_E \\ &= \left(\hat{E}\hat{a} - \hat{a}\hat{E} + \hat{a}\hat{E} \right)\phi_E \\ &= \left(-\hbar\omega\hat{a} + \hat{a}\hat{E} \right) \phi_E \\ &= (E - \hbar\omega)\hat{a}\phi_E \\ &= (E - \hbar\omega)\psi \end{align} It turns out \(\hat{a}\phi_E\) is also an eigenstate of the energy operator! As the energy value is lowered by \(\hbar\omega\), \(\hat{a}\) is called the lower ladder.Similarly, if $$\hat{a}^{+}\phi_E = \psi'$$ Then, $$\hat{E}\psi' = (E + \hbar\omega)\psi'$$ Thus, \(a^{+}\) is called the upper ladder.
Ground State
When \(\hat{a}\) has subtracted the eigenvalue to zero $$\hat{a}\phi_0 = 0$$ we can solve for the eigenstate $$\phi_0 = Ce^{-\frac{\hat{x}}{x_0}}$$ Since \begin{align} < E>&= \int dx \phi^*\hat{E}\phi \\ &= \int dp|\tilde{\Psi}(p)|^2 \frac{p^2}{2m} + \int |\Psi(x)|^2\frac{m\omega^2}{2}x^2 \\ \end{align} We know that energy expectation is non-negative. If the energy eigenvalue \(E \neq (n)\hbar\omega\), for some non-negative integer \(n\), such that \(\hat{a}\) can never subtract \(E\) to zero, the set of energy eigenvalues have no lower bound. The expectation value of \(E\) cannot be positive, which violates our calculation. So, \(E\) must be of \(n \hbar \omega \) and \(\hat{a}\phi_E\) must come to zero eventually. So, the set of the eigenstates found by the ladder operators are all the eigenstates of the harmonic oscillator.


Comments
Post a Comment