Dipole
Dipole Definition
From multipole expansion, the second term is called the dipole potential $$V_{dip}(\textbf{r}) = \frac{1}{4\pi\epsilon_0}\frac{1}{r^2}\int r'\cos\theta\rho(\textbf{r}')d\tau$$ where $$r'\cos\theta = \hat{\textbf{r}}\cdot\textbf{r}'$$ So, dipole potential can be expressed as $$V_{dip}(\textbf{r}) = \frac{1}{4\pi\epsilon_0}\frac{1}{r^2}\hat{\textbf{r}}\cdot\int \textbf{r}'\rho(\textbf{r}')d\tau$$ The dipole moment is defined as $$ \bbox[5px,border:2px solid #666] { \textbf{p} = \int\textbf{r}'\rho(\textbf{r}')d\tau } $$ or for discrete charge distribution $$ \bbox[5px,border:2px solid #666] { \textbf{p} = \sum_{i=1}^nq_i\textbf{r}_i'. } $$When the total net charge is zero, we know, by the multipole expansion, that the dipole potential term is the dominant term. When far away, the potential is approximately equal to the dipole potential.
When the charge source is a perfect dipole, i.e. \(p\) is finite while \(r'\) is zero, then the higher order terms in the multipole expansion are all zero, then the potential is exactly equal to the dipole potential.
Find a simple approximate formula for the potential, valid at points far from the origin.
Solution: The potential is approximately equal to $$V\approx \frac{1}{4\pi\epsilon_0}\frac{\vec{p}\cdot\hat{r}}{r^2}$$ As \begin{align} \vec{p} &= (3qa - qa)\hat{z}+(-2qa-2q(-a))\hat{y} = 2qa\hat{z}\\ \hat{p}\cdot\hat{r} &= 2qa\hat{z}\cdot\hat{r}\\ &= 2qa\cos\theta \end{align} the potential is approximately $$V\approx \frac{1}{4\pi\epsilon_0}\frac{2qa\cos\theta}{r^2}$$
A spherical shell of radius \(R\), which carries a surface charge \(\sigma = k\cos\theta\). Calculate the dipole moment of this charge distribution. Find the approximate potential, at points far from the sphere.
As the the charge distribution is symmetric along z-axis, so is the dipole moment. \begin{align} \vec{p} &= p\hat{z}\\ p &= \int z\rho d\tau = \int z\sigma da\\ &= \int (R\cos\theta)(k\cos\theta)R^3\sin\theta d\theta d\phi \\ &= 2\pi R^3 k \int^{\pi}_0 \cos^2\theta \sin\theta d\theta \\ &= 2\pi R^3 k \left[-\frac{\cos^3\theta}{3}\right]^\pi_0\\ &= \frac{2}{3}\pi R^3k[1-(-1)]\\ &= \frac{4\pi R^3 k}{3} \end{align} So, $$\vec{p} = \frac{4}{3}\pi R^3 k \hat{z}$$
Electric Field of a Dipole
A pure dipole potential is $$V=\frac{\hat{r}\cdot\vec{p}}{4\pi\epsilon_0 r^2} = \frac{p\cos\theta}{4\pi\epsilon_0 r^2}$$ The electric field of the dipole is \begin{align} E_r &= -\frac{\partial V}{\partial r} \\ E_{\theta} &= -\frac{1}{r}\frac{\partial V}{\partial \theta}\\ E_{\phi} &= -\frac{1}{r\sin\theta}\frac{\partial V}{\partial \phi} = 0 \end{align} So, $$ \bbox[5px,border:2px solid #666] { \vec{E}(r,\theta) = \frac{p}{4\pi\epsilon_o r^3}(2\cos\theta \hat{r} + \sin \theta \hat{\theta}) } $$Induced dipole
An atom, though electrical neutral, consists of positive nucleus part and the negative electron part. When put under electric field, atom will be stressed and form a dipole. The induced dipole is roughly proportional to the electric field $$\textbf{p} = \alpha \textbf{E}$$Polar Molecules
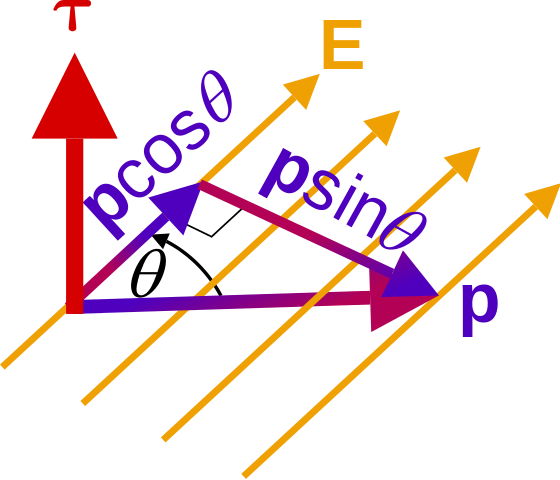
For molecules with built-in permanent dipole moment, when exposed in an external electric field \(\vec{E}\), the torque due to its \(+q\) and \(-q\) poles separated by \(\textbf{d}\) is \begin{align} \vec{N} &= (\vec{r}_+ \times \vec{F}) + (\vec{r}_- \times \vec{F}) \\ &= (\frac{\vec{d}}{2} \times (q\vec{E})) + (\frac{-\vec{d}}{2} \times (-q\vec{E})) \\ &= q\vec{d} \times \vec{E} \\ &= \vec {p} \times \vec{E} \end{align} The force added on the dipole by the E-field is \begin{align} \vec{F} &= \vec{F}_+ + \vec{F}_- \\ &= q(\vec{E}_+ - \vec{E}_-) \\ \end{align} If the dipole is small, we may write $$\vec{E}_+ - \vec{E}_- = (\nabla E_x) \cdot \vec{d} = (\vec{d}\cdot \nabla)\vec{E}$$ Then, $$\vec{F} = (\vec{p} \cdot \nabla)\vec{E}$$Find the torque on \(\vec{p}_1\) due to \(\vec{p}_2\) and the torque on \(\vec{p}_2\) and \(\vec{p}_1\).
Solution: Field of \(\vec{p}_1\) at \(\vec{p}_2\) is $$\vec{E}_1=\frac{p_1}{4\pi\epsilon_0r^3}\left(2\cos\left(\frac{\pi}{2}\right)\hat{r} + \sin\left(\frac{\pi}{2}\right)\hat{\theta}\right)=\frac{p_1}{4\pi\epsilon_0r^3}\hat{\theta}$$ pointing downward. So, torque on \(\vec{p}_2\) is $$\vec{N}_2=\vec{p}_2\times \vec{E}_1=p_2E_1\sin\frac{\pi}{2}=p_2E_1=\frac{p_1p_2}{4\pi\epsilon_0 r^3}$$ Field of \(\vec{p}_2\) at \(\vec{p}_1\) is $$\vec{E}_2=\frac{p_2}{4\pi\epsilon_0r^3}\left(2\cos\left(\pi\right)\hat{r} + \sin\left(\pi\right)\hat{\theta}\right)=\frac{p_1}{4\pi\epsilon_0r^3}(-2\hat{r})$$ pointing downward. So, torque on \(\vec{p}_1\) is $$\vec{N}_1=\vec{p}_1\times \vec{E}_2=p_1E_2\sin\left(-\frac{\pi}{2}\right)=-p_1E_2=\frac{2p_1p_2}{4\pi\epsilon_0 r^3}$$
A (perfect) dipole \(\vec{p}\) is situated a distance \(z\) above an infinite grounded conducting plane. Find the torque on \(\vec{p}\)
Using an image dipole, the electric field on the dipole due to the grounded conducting plane is $$\vec{E}_i = \frac{p}{4\pi\epsilon_0(2z)^3}(2\cos\theta\hat{r}+\sin\theta\hat{\theta})$$ The torque is then \begin{align} \vec{N} &= \vec{p}\times\vec{E}_i = \frac{p^2}{4\pi\epsilon_0(2z)^3}\left(\cos\theta\hat{r} + \sin\theta\hat{\theta})\times(2\cos\theta\hat{r}+\sin\theta\hat{\theta})\right]\\ &= \frac{p^2}{4\pi\epsilon_0(2z)^3}\left[\cos\theta\sin\theta\hat{\phi}+2\sin\theta\cos\theta(-\hat{\phi})\right]\\ &= \frac{p^2\sin\theta\cos\theta}{4\pi\epsilon_0(2z)^3}(-\hat{\phi})\\ &= \frac{p^2\sin 2\theta}{4\pi\epsilon_0(16z^3)}(-\hat{\phi}) \end{align} pointing out of the page.





Comments
Post a Comment