Lagrangian Mechanics

Lagrangian

Lagrangian is defined as $$L = T -V$$ where $T$ is the kinetic energy and $V$ is the potential energy.

When there is no non-conservative force, the Euler-Lagrange equation (Lagrange's equation) holds $$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q_j}}\right) = \frac{\partial L}{\partial q_j}$$ where $q_j$ belongs to a set of generalized coordinates. The Lagrange's equation will yield the equation of motion in Newton's second law. No new physics here. It is useful when we do not know the constraint force.

Checkpoint

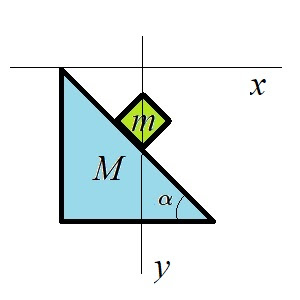
A block of mass m is placed on a frictionless incline of mass M, which is placed on a frictionless horizontal surface. Both the block and the incline are at rest. At time t=0, they are released to move freely. Using the coordinate set as shown in the image below , find the equations of motion of the block and the incline.

The constraint is $$\frac{0-y_2}{x_2-x_1}=\tan\alpha,$$ that is $$\begin{align} y_2 &= (x_1 - x_2)\tan\alpha \\ \dot{y_2} &= (\dot{x_2} - \dot{x_2})\tan\alpha \end{align}$$ The kinetic energy is $$T=\frac{1}{2}M\dot{x}^2_1+\frac{1}{2}m(\dot{x}^2_2+\dot{y}^2_2)$$ and the potential energy is $$V = mgy_2$$ As $y_2$ is dependent variable according to the constraint, it has to be expressed in terms of $x_1$ and $x_2$ in the Lagrangian $$\begin{align} L &= T - V \\ &= \frac{1}{2}M\dot{x}^2_1+\frac{1}{2}m(x^2_2+y^2_2) +mgy_2\\ &= \frac{1}{2}M\dot{x}^2_1+\frac{1}{2}m(\dot{x}^2_2+\tan^2\alpha(\dot{x}_1-\dot{x}_2)^2)-mg\tan\alpha(x_1-x_2). \end{align}$$ Hence, the equations of motion are $$\begin{align} \frac{d}{dt}\frac{\partial L}{\partial \dot{x}_1} - \frac{\partial L}{\partial x_1} &= 0\\ m \tan^2\alpha (\ddot{x_1} - \ddot{x_2}) + M\ddot{x_1} &= -mg \tan \alpha \\ \ddot{x_1}(m\tan^2\alpha + M) &= m\tan^2\alpha\ddot{x_2} - mg\tan\alpha \\ \ddot{x_1} &= \frac{m\tan\alpha(\tan\alpha\ddot{x_2}-g)}{m\tan^2\alpha + M}. \tag{1} \end{align}$$
$$\begin{align} \frac{d}{dt}\frac{\partial L}{\partial \dot{x}_2} - \frac{\partial L}{\partial x_2} &= 0\\ m\ddot{x_2} - (\ddot{x_1}-\ddot{x_2})\tan^2\alpha &= mg \tan\alpha \\ \ddot{x_2}(1+\tan^2\alpha) &= \tan^2\alpha\ddot{x_1} + g\tan\alpha\\ \ddot{x}_2 &= \sin^2\alpha\ddot{x_1} + g\sin\alpha\cos\alpha. \tag{2}\\ \end{align}$$ Substitute (2) into (1), we have $$\ddot{x}_1=-\frac{mg\sin\alpha\cos\alpha}{M+m\sin^2\alpha}$$ and $$\ddot{x}_2 = \frac{Mg\sin\alpha\cos\alpha}{M+m\sin^2\alpha}.$$ By the constraint, $$\ddot{y}_2=-\frac{(M+m)g\sin^2\alpha}{M+m\sin^2\alpha}$$

Noether's Theorem

When a mathematical object is invariant under a transformation, we say that the mathematical object has a symmetry. When a mathematical object is invariant in time at any point of its motion path, we say that the mathematical object is conserved. Action is defined as $$S \equiv \int^{t_2}_{t_1} L(q(s), \dot{q}(s))dt$$ Suppose the action has a symmetry under a transformation $q \to q'$ and $\epsilon(q) \equiv q' - q$, i.e. $$\begin{align} \delta S &= 0\\ &= \int^{t_2}_{t_1} \left( \frac{\partial L}{\partial q}\epsilon + \left(\frac{\partial L}{\partial \dot{q}}\right)\frac{d\epsilon}{dt}\right) dt \\ \end{align}$$ Integrating the second term by part, $$\int \left(\frac{\partial L}{\partial \dot{q}}\right)\frac{d\epsilon}{dt} dt = \frac{\partial L}{\partial \dot{x}}\epsilon - \int \left(\epsilon\frac{d}{dt}\frac{\partial L}{\partial \dot{q}}\right) dt$$ we have $$0 = \left[\epsilon\frac{\partial L}{\partial \dot{q}}\right]^{t_2}_{t_1} + \left[\int^{t_2}_{t_1}\epsilon\left(\frac{\partial L}{\partial q} - \frac{d}{dt}\frac{\partial L}{\partial \dot{q}}\right) dt \right]$$ As Lagrangian is defined such that it satisfies the relationship $$\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}}\right) - \frac{\partial L}{\partial q} = 0$$ so $$\left[\frac{\partial L}{\partial \dot{q}}\epsilon\right]^{t_2}_{t_1} = 0$$ for arbitrary $t_2$ and $t_1$, i.e. $$\frac{\partial L}{\partial \dot{q}}\epsilon$$ is constant over time. This is called the Noether's theorem.

Coupled Oscillations

The Lagrangian of the system is $$\begin{align} L &= T - V \\ &= \left( \frac{1}{2}m\dot{x_1}^2 + \frac{1}{2}m\dot{x_2}^2 \right) \\ &- \left( \frac{1}{2}Kx_1^2 + \frac{1}{2}K'\left(x_2 - x_1\right)^2 + \frac{1}{2}Kx_2^2 \right) \end{align}$$ The Lagrange's equations are then solved to give the equations of motion $$\begin{align} m\ddot{x_1} + (K + K')x_1 - K'x_2 &= 0 \\ m\ddot{x_2} - K'x_1 + (K + K')x_2 &= 0 \\ \end{align}$$ Adding and subtracting the two equations $$\begin{align} m(\ddot{x_2} + \ddot{x_1}) + K(x_2 + x_1) &= 0 \\ m(\ddot{x_2} - \ddot{x_1}) + (K +2K')(x_2 - x_1) &= 0 \\ \end{align}$$ Let $$Q_1 \equiv x_2 + x_1$$ and $$Q_2 \equiv x_2 - x_1$$ The equations of motion become $$\begin{align} m\ddot{Q_1} + KQ_1 &= 0 \\ m\ddot{Q_2} + (K +2K')Q_2&= 0 \\ \end{align}$$ Their general solutions are $$\begin{align} Q_1(t) &= a_1 \cos(\omega_1 t - \delta_1) & \text{ where } \omega_1^2 = \frac{K}{m}\\ Q_2(t) &= a_2 \cos(\omega_2 t - \delta_2) & \text{ where } \omega_2^2 = \frac{K+2K'}{m}\\ \end{align}$$ $Q_1$ and $Q_2$ are called the normal mode coordinates. $\omega_1$ and $\omega_2$ are called normal mode frequencies. We have the solutions $$\begin{align} x_1(t) &= \frac{Q_1 - Q_2}{2} = \frac{a_1}{2} \cos(\omega_1 t - \delta_1) - \frac{a_2}{2} \cos(\omega_2 t - \delta_2) \\ x_2(t) &= \frac{Q_1 + Q_2}{2} = \frac{a_1}{2} \cos(\omega_1 t - \delta_1) + \frac{a_2}{2} \cos(\omega_2 t - \delta_2) \\ \end{align}$$

Example

Two pendulums of length $l$ and masses $m$ are connected with a massless spring with spring constant $k$ and relaxed length $d$. Find the general solution of the motion of the masses in small oscillation.

Solution: The coordinates of the two masses are $$\begin{cases} x_1 = l\sin\theta_1\\ y_1 = -l\cos\theta_1 \end{cases}$$ and $$\begin{cases} x_2 = d + l\sin\theta_2\\ y_2 = -l \cos\theta_2. \end{cases}$$ Their velocities are $$\begin{cases} \dot{x}_1 = l\dot{\theta}_1\cos\theta_1\\ \dot{y}_1 = l\dot{\theta}_1\sin\theta_1 \end{cases}$$ and $$\begin{cases} \dot{x}_2 = l\dot{\theta}_2\cos\theta_2\\ \dot{y}_2 = l\dot{\theta}_2\sin\theta_2 \end{cases}$$ The distance between the masses is $$\begin{align} s&=\sqrt{(y_1-y_2)^2+(x_1-x_2)^2}\\ &=\sqrt{l^2(\cos\theta_1-\cos\theta_2)^2+(l\sin\theta_1-l\sin\theta_2-d)^2}\\ &=\sqrt{2l^2-2l^2\cos(\theta_1-\theta_2)-2dl(\sin\theta_1-\sin\theta_2)+d^2} \end{align}$$ As the oscillation is small, applying Taylor series approximation, we have $$\cos(\theta_1-\theta_2) \approx 1 - \frac{1}{2}(\theta_1-\theta_2)^2$$ and $$\sin\theta_1-\sin\theta_2=\theta_1-\theta_2.$$ So, $$s \approx \sqrt{l^2(\theta_1-\theta_2)^2+2dl(\theta_2-\theta_1)+d^2}=l(\theta_2-\theta_1)+d$$ The kinetic energy of the system is $$\begin{align} T &= \frac{1}{2}m(\dot{x}^2_1+\dot{y}^2_1)+\frac{1}{2}m(\dot{x}^2_2+\dot{y}^2_2)\\ &= \frac{1}{2}ml^2\dot{\theta}^2_1+\frac{1}{2}ml^2\dot{\theta^2_2}\\ &= \frac{1}{2}ml^2\left(\dot{\theta}^2_1+\dot{\theta}^2_2\right)\\ \end{align}$$ and the potential energy of the system is $$\begin{align} V &= \frac{1}{2}k(s-d)^2+mgy_1+mgy_2\\ &= \frac{1}{2}kl^2(\theta_2-\theta_1)^2-mgl\cos\theta_1-mgl\cos\theta_2\\ &= \frac{1}{2}kl^2(\theta_2-\theta_1)^2-mgl(1-\frac{1}{2}\theta^2_1)-mgl(1-\frac{1}{2}\theta^2_2) \end{align}$$ So, the Lagrangian is $$L=T-V=\frac{1}{2}ml^2\left(\dot{\theta}^2_1+\dot{\theta}^2_2\right)\\ -\frac{1}{2}kl^2(\theta_2-\theta_1)^2+mgl(1-\frac{1}{2}\theta^2_1)+mgl(1-\frac{1}{2}\theta^2_2)$$ The equations of motion are $$\begin{align} \frac{d}{dt}\frac{\partial L}{\partial \dot{\theta}_1}=\frac{\partial L}{\partial \theta_1} &\implies ml^2\ddot{\theta_1}-kl^2(\theta_2-\theta_1)+mgl\theta_1=0\\ \frac{d}{dt}\frac{\partial L}{\partial \dot{\theta}_2}=\frac{\partial L}{\partial \theta_2} &\implies ml^2\ddot{\theta_2}+kl^2(\theta_2-\theta_1)+mgl\theta_2=0 \end{align}$$ Assuming the solutions to be $$\begin{align} \theta_1 &= a_1\cos(\omega t-\delta) \\ \theta_2 &= a_2\cos(\omega t-\delta), \end{align}$$ we have $$(ml^2\omega^2-kl^2-mgl)a_1+kl^2a_2 = 0\\ kl^2a_1+(ml^2\omega^2-kl^2-mgl)a_2=0$$ To have non-trivial solutions, $$\begin{align} \begin{vmatrix} ml^2\omega^2-kl^2-mgl & kl^2 \\ kl^2 & ml^2\omega^2-kl^2-mgl \\ \end{vmatrix} &=0\\ (ml^2\omega^2-mgl)(ml^2\omega^2-2kl^2-mgl)&=0 \end{align}$$ So, $$\omega^2=\frac{g}{l}$$ or $$\omega^2=\frac{g}{l}+\frac{2k}{m}$$ For $\omega^2 = \frac{g}{l}$, substitute into equation of motion, $$\begin{align} (ml^2\omega^2-kl^2-mgl)a_1+kl^2a_2 &= 0 \\ \left(ml^2\left(\frac{g}{l}\right)-kl^2-mgl\right)a_1+kl^2a_2 &= 0\\ a_1&=a_2 \end{align}$$ Similarly, for $\omega^2=\frac{g}{l}+\frac{2k}{m}$, $$a_1=-a_2$$ So, the general solution is $$\begin{bmatrix} \theta_1(t)\\ \theta_2(t) \end{bmatrix} = C \begin{bmatrix} a_1\cos(\omega_1t-\delta_1)\\ a_1\cos(\omega_1t-\delta_1) \end{bmatrix} +D \begin{bmatrix} a_2\cos(\omega_2t-\delta_2)\\ -a_2\cos(\omega_2t-\delta_2) \end{bmatrix},$$ where $C$ and $D$ are constants and $\omega_1 = \sqrt{\frac{g}{l}}$ and $\omega_2=\sqrt{\frac{g}{l}+\frac{2k}{m}}$

Checkpoint

Two beads of equal masses $m$ are put on a frictionless incline and connected by a spring with force constant $k$ and a relaxed length $l_0$. At $t=0$, $x_1'=2l_0$, $x_2'=4l_0$ and both beads are at rest. Find $x_1'(t)$ and $x_2'(t)$ as a function of time.

The kinetic energy of the system is $$T=\frac{1}{2}m\dot{x}_1^2+\frac{1}{2}m\dot{x}_2^2$$ and the potential energy of the system is $$V=mgx_1'\sin\theta+mgx_2'\sin\theta+\frac{1}{2}k(x_2'-x_1'-l_0)^2$$ So, the Lagrangian is $$L=T-V=\frac{1}{2}m\dot{x}_1^2+\frac{1}{2}m\dot{x}_2^2\\ -\left[mgx_1'\sin\theta+mgx_2'\sin\theta+\frac{1}{2}k(x_2'-x_1'-l_0)^2\right]$$ The equations of motion are $$\begin{align} \frac{d}{dt}\frac{\partial L}{\partial \dot{x}_1'}=\frac{\partial L}{\partial x_1'} &\implies m\ddot{x}_1'=-mg\sin\theta+k(x_2'-x_1'-l_0)\\ \frac{d}{dt}\frac{\partial L}{\partial \dot{x}_2'}=\frac{\partial L}{\partial x_2'} &\implies m\ddot{x}_2' = -mg\sin\theta-k(x_2'-x_1'-l_0) \end{align}$$ Subtracting the two equations, $$\ddot{x}_1'-\ddot{x}_2'=\left(\frac{2k}{m}\right)(x_2'-x_1'-l_0)$$ Let $$Q=x_2'-x_1'-l_0$$ The equations of motion become $$\ddot{Q}=-\frac{2k}{m}Q$$ The general solution is $$Q(t)=a\cos(\omega t + \delta)$$ Applying initial conditions, $$Q(t)=x_2'(t)-x_1'(t)-l_0=l_0\cos\left(\sqrt{\frac{2k}{m}}t\right)$$ Thus, $$\ddot{x}_1' = -g\sin\theta+\left(\frac{kl_0}{m}\right)\cos\left(\sqrt{\frac{2k}{m}}t\right).$$ Hence, $$x'_1(t) = -gt^2\sin\theta + at +b -\frac{l_0}{2}\cos\left(\sqrt{\frac{2k}{m}}t\right)$$ Applying initial conditions, $$\begin{align} x_1' &= -gt^2\sin\theta - \frac{l_0}{2}\cos\left(\sqrt{\frac{2k}{m}}t\right)+\frac{5}{2}l_0\\ x_2' &= -gt^2\sin\theta + \frac{l_0}{2}\cos\left(\frac{2k}{m}t\right) + \frac{7}{2}l_0 \end{align}$$